Expondremos las ecuaciones para el aire húmedo.
EL VOLUMEN
POTENCIALES QUIMICOS
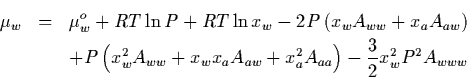
POTENCIALES QUIMICOS DEL AGUA CON AIRE DISUELTO
Sabemos que cuando el agua pura está en equilibrio con su vapor tiene que cumplirse:
Esta ecuación es importante pues conocemos
![]() .
Si deseamos calcular el potencial químico fuera de la presión de equilibrio
a una temperatura dada:
.
Si deseamos calcular el potencial químico fuera de la presión de equilibrio
a una temperatura dada:
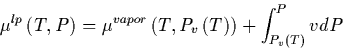
Si consideramos al agua como una mezcla líquida ideal de agua y aire podemos escribir el potencial químico:
Entonces el potencial químico del agua en la mezcla de agua y aire:
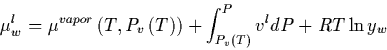
Si consideramos que ![]() es casi independiente de la presión para el
agua líquida:
es casi independiente de la presión para el
agua líquida:
EQUILIBRIO AGUA-AIRE
Para encontrar las concentraciones de equilibrio del sistema debemos igualar los potenciales químicos.
La ecuación de potenciales del gas en ambas fases la reemplazamos por la
ecuación de la solubilidad del aire en agua:
![]() Igualando los potenciales químicos del agua en ambas fases y reemplazando
Igualando los potenciales químicos del agua en ambas fases y reemplazando ![]() llegamos a:
llegamos a:
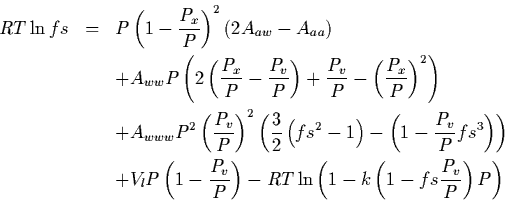
donde
![]() ,
,
![]() es el volumen del líquido y
es el volumen del líquido y ![]() es la solubilidad del aire en agua.
es la solubilidad del aire en agua.
Esta ecuación debe ser iterada, pero si hacemos ![]() obtenemos de entrada
una primera aproximación bastante buena, así procede el [1]
que escribe la ecuación con esta simplificación
efectuada y reemplaza el logaritmo por una aproximación
(la edición que tengo tiene algunos errores de tipeo).
El Psicro.bas itera pues con muy pocos ciclos converge.
obtenemos de entrada
una primera aproximación bastante buena, así procede el [1]
que escribe la ecuación con esta simplificación
efectuada y reemplaza el logaritmo por una aproximación
(la edición que tengo tiene algunos errores de tipeo).
El Psicro.bas itera pues con muy pocos ciclos converge.