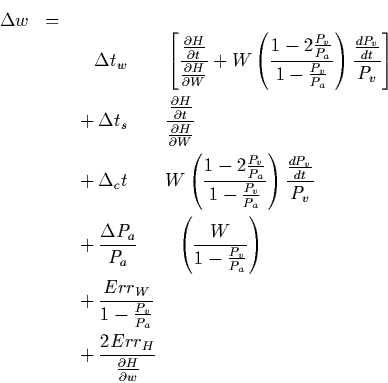Next: CONCLUSIONES.
Up: PROPAGACION DE ERRORES EN
Previous: ERRORES EN LA ENTALPIA.
Además de calcular los errores con las ecuaciones aproximadas se despreciará
la entalpía del agua involucrada, entonces:
Se aplicará la siguiente notación:
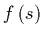 será la función
será la función
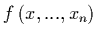 evaluada en
evaluada en 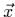 correspondiente al aire
con su humedad y su temperatura
correspondiente al aire
con su humedad y su temperatura
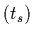 ;
;
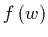 será
será
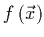 evaluada para el aire
saturado con temperatura
evaluada para el aire
saturado con temperatura 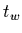 .
Si la
.
Si la
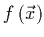 se encuentra derivada, se entenderá
que a la derivada de la función
se encuentra derivada, se entenderá
que a la derivada de la función
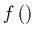 deberá tomársela
en la condición
deberá tomársela
en la condición 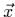 .
Luego se aproxima igualando:
.
Luego se aproxima igualando: 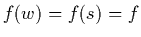 .
Analizaremos las primeras diferenciales:
.
Analizaremos las primeras diferenciales:
aproximando y desarrollando el
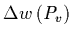
ordenando queda:
root
2000-10-22
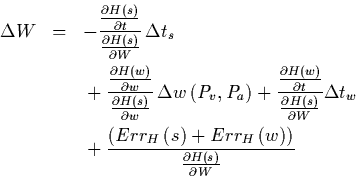
![\begin{eqnarray*}
\Delta W &=& \frac{\depa{H}{t}}{\depa{H}{W}} \left(\Delta t_w...
...Err_W}{W} \big] \\
&& \mbox{} + 2 \frac{Err_H}{\depa{H}{W}}
\end{eqnarray*}](img45.gif)